Polynomials Class-10th Board: A polynomial is an algebraic expression that consists of variables and coefficients, involving operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. The chapter aims to introduce students to the concept, types, and applications of polynomials, which is a crucial topic in algebra.
Table of Contents
Polynomials Full Chapter Class 10 Board Exam
Learn C Programming tutorial in detailed by jng academy.
What is Polynomials Class-10th Board
It is an algebraic expression that consists of variables and coefficients, involving operations of addition, subtration, multiplication, and non-negative integer exponents of variables.
A polynomial is an expression of the form:
P(x) = anxn + an-1xn-1 + . . . + a1x1 + a0
Where, an , an-1 , . . . , a1 , a0 are constants, and n is a non-negative integer called the degree of the polynomial.

Types of Polynomials Class-10th Board
- Constant Polynomial: A polynomial of degree 0, e.g., P(x) = c.
- Linear Polynomial: A polynomial of degree 1, e.g., P(x) = ax + c.
- Quadratic Polynomial: A polynomial of degree 2, e.g., P(x) = ax2 + bx + c.
- Cubic Polynomial: A polynomial of degree 3, e.g., P(x) = ax3 + bx2 + cx + d.
Degree of a polynomial
The degree of a polynomial is the highest power of the variable in the expression.
Example: P(x) = ax3 + bx2 + cx + d. in this example the degree is 3.
Example: P(x) = bx2 + cx + d. in this example the degree is 2.
Zeros/Roots of a Polynomial Class-10th Board
The value of x for which P(x) = 0 are called the zeros or roots of the polynomial.
For a quadratic polynomial ax2 + bx + c = 0, the quadratic formula is used to find the roots:
x = {-b ± root(D)}/2a where D is discreminent and value D = root(b2 – 4ac)
Example: The polynomial x2 -3x + 2 has roots x = 1 and x = 2.
Division of Polynomial
Polynomial Long Division: Used to divide one polynomial by another. If P(x) is divided by g(x), the division algorithm states:
P(x) = g(x).q(x) + r(x) or Dividend = Divisor * Quotient + Remainder
where q(x) is the quotient and r(x) is the remainder, with deg(r(x)) < deg(g(x)).
Example:
Divide 2x2 + 3x + 1 by x + 2.
Solution:
Image Coming Soon…
Example:
Divide 3x3 + x2 + 2x + 5 by 1 + 2x + x2
Solution:
Image Coming Soon…
Example:
Divide 3x2 – x3 – 3x + 5 by x – 1 – x2 , and verify the division algorithm.
Solution:
Image Coming Soon…
Example:
Find all the zeroes of 2x4 – 3x3 – 3x2 + 6x – 2, if you know that two of its zeroes are √2 and -√2.
Solution:
Image Coming Soon…
Relationship Between Coefficients and Roots
For a quadratic polynomial P(x) = ax2 + bx + c, the sum and poduct of the roots can be derived using:
Sum of the roots (α+β) = -b/a
Product of the roots (α.β) = c/a
Example:
Find the zeroes of the quadratic polynomial x2 + 7x + 10, and verify the relationship between the zeroes and the coefficients.
Solutions:
Given, Quadratic Polynomial x2 + 7x + 10.
x2 + 7x + 10 = (x + 2)(x + 5)
Here, a = 1, b = 7 and c = 10
So, the value of x2 + 7x + 10 is zeroes when x + 2 = 0 or x + 5 = 0, i.e., when x = -2 or x = -5. Therefore, the zeroes of x2 + 7x + 10 are -2 and -5. Now,
Sum of the roots (α+β) = -b/a = -7/1 = -7
Product of the roots (α.β) = c/a = 10/1 = 10
Clearly see that sum of the roots i.e., -2 and -5 = -7 and Products of the roots = -2 * -5 = 10.
Hence, we can clearly say that it is verify the relationship between the zeroes and the coeffiencts.
Cubic Polynomial:
In general, it can be proved that if α, β and γ are the zeroes of the cubic polynomial ax3 + bx2 + cx + d, then
α + β + γ = -b/a
αβ + βγ + γα = c/a
αβγ = -d/a
Geometrical Meaning of the Zeroes of a Polynomials Class-10th Board
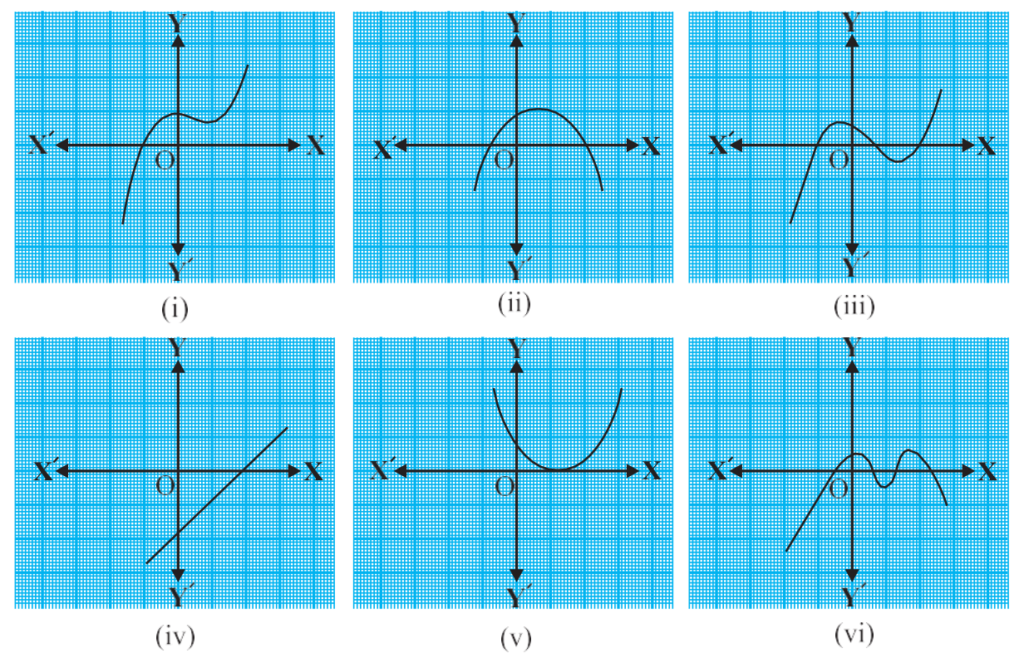
We know that a real number k is a zero of the polynomial p(x) if p(k) = 0. Below graphical examples are taken by ncert book of class-10th mathematics here we will try to find out the number of zeroes of each graph one by one. The concepts to find the number of zeroes from a graph is very simple we need check first how many times functions or polynomial graph cuts the x-axis we don’t need to bother about y-axis we need to check only x-axis. If we found that number of times graph or polynomial graph cuts the x-axis the we can easily find out the number of zeroes.
There is very easy concepts, Number of zeroes is equal to number of cuts/intersects on x-axis by the graph.
In simple term, Number of zeroes = Number of Cuts/intersects on x-axis by the graph.
So the above concepts we can easily find out the numbers of zeroes of below graph:
- Number of zeroes in (i) = 1 (because p(x) graph cuts/intersects x-axis one time)
- Number of zeroes in (ii) = 2 (because p(x) graph cuts/intersects x-axis two times)
- Number of zeroes in (iii) = 3 (because p(x) graph cuts/intersects x-axis three times)
- Number of zeroes in (iv) = 1 (because p(x) graph cuts/intersects x-axis one time)
- Number of zereos in (v) = 1 (because p(x) graph cuts/intersects x-axis one time)
- Number of zeroes in (vi) = 4 (because p(x) graph cuts/intersects x-axis 4 times)
Important Formulas in Polynomials
Quadratic Formula:
x = {-b ± root(D)}/2a where D is discreminent and value D = root(b2 – 4ac)
Factor Theorem:
If P(x) is a polynomial, and P(a) = 0, then x – a is a factor of P(x).
Remainder Theorem:
If a polynomial P(x) is divided by x – a, then the remainder is P(a).
Application of Polynomials
Roots of Equations:
Polynomials help solve equations arising in various real-life problems, such as motion, economics, and physics.
Geometry:
Polynomials are used in curve fitting and finding the area under curves.
Computer Graphics:
Polynomial equations model curves and surfaces in 3D rendering.
Frequently Asked Questions (FAQs)
What is a polynomial?
What are the different types of polynomials?
Constant Polynomial: Degree 0 (e.g., P(x) = 10)
Linear Polynomial: Degree 1 (e.g., P(x) = 2x + 10)
Quadratic Polynomial: Degree 2 (e.g., P(x) = x2 + 5x + 2)
Cubic Polynomial: Degree 3 (e.g., P(x) = ax3 + bx2 + cx + d )
How do you find the degree of a polynomial?
What are the zeros or roots of a polynomial?
What is the relationship between the roots and coefficients of a quadratic polynomial?
Sum of the roots (α+β) = -b/a
Product of the roots (α.β) = c/a
What is the Factor Theorem?
How do you divide polynomial?
How do you divide polynomial?
Can polynomials have negative or fractional exponents?
What is a quadratic polynomial?
What is the significance of the degree of a polynomial?
Learn More
Subscribe “JNG ACADEMY” for more learning best content.
Important Links
C Programming Language Lecture-01
C Programming Language Lecture-02
C Programming Language Lecture-03
C Programming Language Lecture-04
C Programming Language Lecture-05
C Programming Language Lecture-06
C Programming Language Lecture-07
C Programming Langauge Lecture-08
Thank You So Much, Guys… For Visiting our Website and Youtube.
