Pair of Linear Equations in Two Variables Class-10th Baord : This post provides a comprehensive overview of the pair of linear equations in two variables. With multiple methods of solving and real-world applications, it is a vital concept for students to master.
Class 10th BSEB Board PYQs Solution and Answer Key
Table of Contents
Pair of Linear Equations in Two Variables Class-10th Board
In mathematics, a pair of linear equations in two variables represents two equations, each involving two unknowns, typically denoted as x and y. The general form of such equations is:
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
where a1, b1, c1, a2, b2, and c2 are real numbers, and x and y are the variables we nee to solve for.
Solution of a pair of Linear Equations
The solution to a pair of linear equations is a set of values for x and y that satisfies both equations simultaneously. Geometrically, the solution corresponds to the point(s) where the two lines (represented by the equations) intersect on the Cartesian plane.
There are three possibilities for the solutions of a pair of linear equations:
- Unique solution: The lines intersect at exactly one point.
- Infinitely many solutions: The lines are coincident (overlapping), meaning every point on the line satisfies both equations.
- No solution: The lines are parallel and never intersect.
Methods of Solving Pair of Linear Equations in Two Variables Class-10th Board
There are several algebraic methods to solve a pair of linear equations:
Graphical Method:
In this method, both equations are graphed as straight lines on the coordinate plane. The solution is the point of intersection of the two lines.
- If the lines intersect at a point, that point gives the unique solution.
- If the lines are parallel, there is no solution.
- If the lines coincide, there are infinitely many solutions.
Substitution Method:
In this method:
- Solve one of the equations for one variable in terms of the other.
- Substitute this expression into the second equation and solve for the remaining variable.
- Use the obtained value to find the value of the first variable.
Elimination Method:
The elimination method involves eliminating one of the variables by adding or subtracting the equations.
- Multiply one or both equations (if needed) so that the coefficients of one of the variables become equal.
- Add or subtract the equations to eliminate that variable.
- Solve the resulting equation for the remaining variable, and substitute back to find the other variable.
Cross-Multiplication Method:
This method uses a formula to directly solve for x and y. For the system:
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
The values of x and y are calculated as:
x = (b1c2 – b2c1)/(a1b2 – a2b1) and y = (c1a2 – c2a1)/(a1b2 – a2b1)
This method is particularly useful when the equations are complex and involve fractions.

Consistency of the System
The nature of solutions of a pair of linear equations can be determined based on the values of a1/a2, b1/b2, c1/c2:
- Unique Solution: If a1/a2 ≠ b1/b2, the lines intersect at one point.
- Infinitely many solutions: If a1/a2 = b1/b2 = c1/c2, the lines coincide.
- No Solution: If a1/a2 = b1/b2 ≠ c1/c2, the lines are parallel.
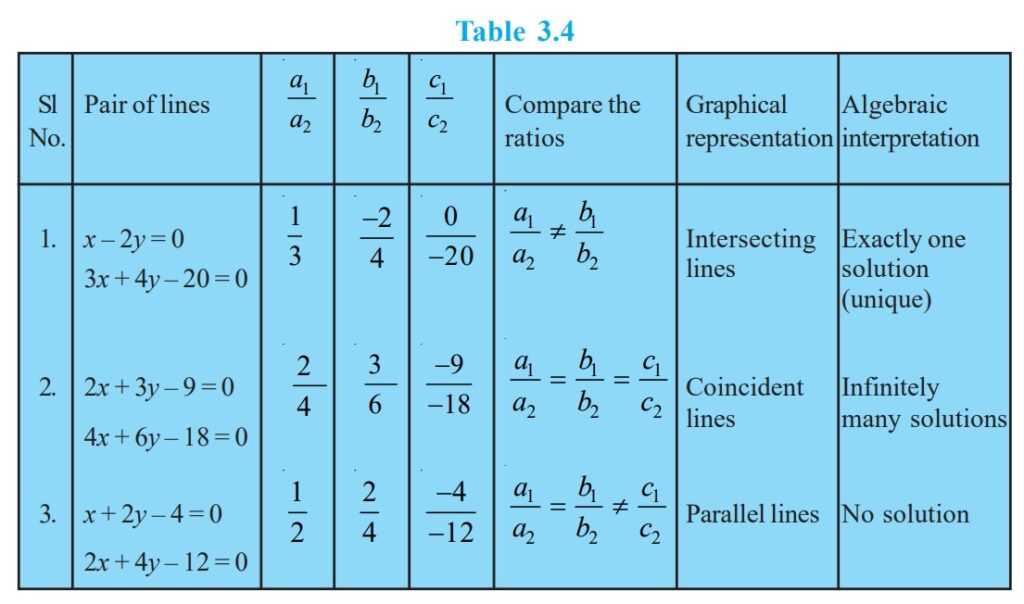
Above image you all know that this is important image from NCERT, in this image we compare graphical representation and algebraic interpretation.
Applications
Pairs of linear equations have many real-world applications. They are used to solve problems involving:
- Calculating the break-even point in business (profit and cost equations).
- Solving speed and distance problems in physics and daily life.
- Optimizing solutions in economics, logistics, and scheduling.
Example
Solve the following system of equations using the substitution method:
2x + 3y – 9 = 0 and 4x – y – = 0
Solutions:
Let 2x + 3y – 9 = 0 is equation (i) and 4x – y -3 = 0 is equation (ii)
From equation (ii), you get
y = 4x – 3 . . . (iii)
Now, Substitute this equation i.e., equation (iii) into equation (i):
2x + 3(4x – 3) – 9 = 0
2x + 12x – 9 – 9 = 0
14x – 18 = 0
14x = 18
x = 9/7
Again, Substitute x = 9/7 into equation (iii):
y = 4*9/7 – 3
y = 36/7 – 3
y = (36 – 21)/7
y = 36/7
Therefore, the required solution is x = 9/7 and y = 15/7.
4x – y -3 = 0
Summary
The chapter Pair of Linear Equations in Two Variables introduces the concept of solving two linear equations with two unknowns. It explores different methods of solving these equations, such as the graphical, substitution, elimination, and cross-multiplication methods. The chapter explains how the solutions can represent either a unique solution, no solution, or infinitely many solutions, based on the nature of the lines. It also covers the consistency of the system and highlights practical applications of linear equations in various real-life situations. This chapter builds a foundation for solving algebraic problems efficiently.
Frequently Asked Questions (FAQs)
What is a pair of linear equations in two variables?
a2x + b2y + c2 = 0, where x and y are unknowns.
How many solutions can a pair of linear equations have?
What are the different methods to solve a pair of linear equations?
What is the graphical method of solving linear equations?
What does the consistency of a system of equations mean?
Learn More
Subscribe “JNG ACADEMY” for more learning best content.
Important Links
C Programming Language Lecture-01
C Programming Language Lecture-02
C Programming Language Lecture-03
C Programming Language Lecture-04
C Programming Language Lecture-05
C Programming Language Lecture-06
C Programming Language Lecture-07
C Programming Langauge Lecture-08
Thank You So Much, Guys… For Visiting our Website and Youtube.
